问题的提出

密度矩阵的等变性

  量子化学定义密度矩阵 PP 如下：

Pμν=2∑aN/2CμaCνa∗,orP∝CC† P_{\mu\nu} = 2\sum_{a}^{N/2} C_{\mu a}C_{\nu a}^*, \quad \text{or} \quad P \propto CC^\dagger

其中 Cji,j=1,2,⋯ ,N/2C_{ji}, j = 1,2,\cdots, N/2 是空间轨道 ∣χi⟩|\chi_i\rangle 在基函数 ∣φj⟩|\varphi_j\rangle 下的展开系数，满足∣χi⟩=∑jCji∣φj⟩\displaystyle |\chi_i\rangle = \sum_j C_{ji}|\varphi_j\rangle，NN 是电子数，μ,ν\mu, \nu 是轨道指标。

  在计算中，由于笛卡尔坐标系取向的任意性，对于同一个分子将会有多个等效的密度矩阵。 不同的坐标系通过三维旋转联系（密度矩阵显然具有平移不变性），我们想知道这些密度矩阵之间的联系。

  首先假设，所有的基函数都可以被分解为径向部分和角向部分的张量积，即

∣φ(x,y,z)⟩=∣φ(r,θ,ϕ)⟩=∣R(r)⟩⊗∣Y(θ,ϕ)⟩ |\varphi(x,y,z)\rangle = |\varphi(r, \theta, \phi)\rangle = |R(r)\rangle \otimes |Y(\theta, \phi)\rangle

其中 ∣Y(θ,ϕ)⟩|Y(\theta, \phi)\rangle 是球谐函数，是球面上调和函数类的标准正交基； R(r)R(r) 是径向部分。这样，
三维旋转只对角向部分起作用。在积空间内定义旋转算符 T^(θ,ϕ)=I^⊗R^(θ)R^(ϕ)\hat T(\theta, \phi) = \hat I \otimes \hat R(\theta)\hat R(\phi)，其中 I^\hat I 是径向部分的单位算符，而 R^(θ)=e−i(c1L^xθ1+c2L^yθ2)/ℏ\displaystyle \hat R(\theta) = e^{-i(c_1 \hat L_x \theta_1 + c_2 \hat L_y \theta_2)/\hbar} 是绕 xx 轴和 yy 轴旋转的算符，绕某轴旋转 θ\theta 的效果被分解为绕 x,yx,y 轴旋转θ1,θ2\theta_1, \theta_2，L^x,L^y\hat L_x, \hat L_y 是相应角动量；R^(ϕ)=e−iL^zϕ/ℏ\displaystyle \hat R(\phi) = e^{-i\hat L_z \phi/\hbar} 同理。如此定义的旋转算符，作用效果为：

T^(θ0,ϕ0)∣φ(r,θ,ϕ)⟩=∣φ(r,θ−θ0,ϕ−ϕ0)⟩ \hat T(\theta_0, \phi_0) |\varphi(r, \theta, \phi)\rangle = |\varphi(r, \theta-\theta_0, \phi - \phi_0)\rangle

所以 T^\hat{T} 是酉算符，是保持标准正交基的。由于基的完备性，旋转后的基函数可以被原基组展开，即

∣φj⟩=T^∣φj′⟩=∑kTkj∣φk′⟩ |\varphi_j\rangle = \hat{T} |\varphi_j'\rangle = \sum_{k} T_{kj} |\varphi_{k}'\rangle

同时左乘 ⟨φi′∣\langle \varphi_i' |，得到

⟨φi′∣φj⟩=∑k⟨φi′∣φk′⟩Tkj=∑kδikTkj=Tij⇒∣φj⟩=∑k∣φk′⟩⟨φk′∣φj⟩=∑kTkj∣φk′⟩ \langle \varphi_i' | \varphi_j\rangle = \sum_{k} \langle \varphi_i' | \varphi_k' \rangle T_{kj} = \sum_{k} \delta_{ik} T_{kj} = T_{ij} \quad \Rightarrow \quad |\varphi_j\rangle = \sum_k |\varphi_k'\rangle \langle \varphi_k'| \varphi_j\rangle = \sum_{k} T_{kj} |\varphi_k'\rangle

对于旋转前后的同一个空间轨道 ∣χi⟩|\chi_i\rangle 而言：

∣χi⟩=∑jCji∣φj⟩=∑j,kTkjCji∣φk′⟩=∑kCki′∣φk′⟩⇒C′=TC |\chi_i\rangle = \sum_j C_{ji} |\varphi_j\rangle = \sum_{j,k} T_{kj}C_{ji} |\varphi_k'\rangle = \sum_k C_{ki}' |\varphi_k'\rangle \quad \Rightarrow \quad C' = TC

故旋转前后的密度矩阵之间的关系为

P′=2C′C′†=2(TC)(TC)†=T(2CC†)T†=TPT† P' = 2 C'C'^\dagger = 2(TC)(TC)^\dagger = T(2CC^\dagger) T^\dagger = TP T^\dagger

如此，称密度矩阵是一个等变（equivariant）矩阵，因为在旋转变换下它具有确定的变换规律。

等变映射

  由于密度矩阵独特的变换性质，在针对密度矩阵的预测过程中，我们希望使用预测映射 ff 同样具有内禀的等变数学性质。例如，对于从矢量 vv 到矩阵，或者矩阵 XX 到另一个矩阵的任务，我们分别希望预测映射 f1,f2f_1,f_2 分别满足

f1(Tv)=Tf1(v)T†,f2(TXT†)=Tf2(X)T† f_1(Tv) = Tf_1(v)T^\dagger, \quad f_2(TXT^\dagger) = Tf_2(X)T^\dagger

也即预测映射与旋转操作对易。

密度矩阵的参数化

密度矩阵按照角动量的分块

  对于一个空间轨道系综 {∣χi⟩}\{|\chi_i\rangle\}，完整的密度矩阵定义如下：

P=∑i∣χi⟩⟨χi∣ \boldsymbol{P} = \sum_{i} |\chi_i\rangle \langle \chi_i|

计算化学通常选用的基组是单原子轨道，可以用 n,l,mn,l,m 三个量子数表示。将前述系数矩阵 CC 的第 ii 列按照 n,l,mn,l,m 重新排列，重写分子轨道 ∣χi⟩|\chi_i\rangle 得到

∣χi⟩=∑n∑l,mCnlm(i)∣n,l,m⟩=∑n∑l,mCnlm(i)∣n⟩⊗∣l,m⟩ |\chi_i\rangle = \sum_n\sum_{l,m} C^{(i)}_{nlm} |n,l,m\rangle = \sum_n\sum_{l,m} C^{(i)}_{nlm} |n\rangle \otimes |l,m\rangle

按照前式得到这组基下的密度矩阵

P=∑i∑n1,n2∑l1,l2∑m1,m2Cn1l1m1(i)Cn2l2m2(i)∗∣n1,l1,m1⟩⟨n2,l2,m2∣ \boldsymbol{P} = \sum_i \sum_{n_1,n_2}\sum_{l_1,l_2}\sum_{m_1,m_2} C^{(i)}_{n_1 l_1 m_1} C^{(i)*}_{n_2 l_2 m_2} |n_1, l_1, m_1\rangle \langle n_2, l_2, m_2|

优先对所有的空间轨道 {i}\{i\} 求和，定义 Pm1m2(l1,l2)\displaystyle \mathcal{P}^{(l_1,l_2)}_{m_1m_2} 为

Pm1m2(l1,l2)=∑n1,n2∑iCn1l1m1(i)Cn2l2m2(i)∗∣n1⟩⟨n2∣ \mathcal{P}^{(l_1,l_2)}_{m_1m_2} = \sum_{n_1,n_2}\sum_i C^{(i)}_{n_1 l_1 m_1} C^{(i)*}_{n_2 l_2 m_2} |n_1\rangle \langle n_2|

并交换求和次序，则可按照角动量 ll 的不同将密度矩阵分为若干个如上式的 (l1,l2)(l_1,l_2) 块，其中分量以 m1,m2m_1,m_2 表示，形状为 (2l1+1)×(2l2+1)(2l_1 + 1) \times (2l_2 + 1)：

P=∑l1,l2∑m1,m2Pm1m2(l1,l2)⊙∣l1,m1⟩⟨l2,m2∣ \boldsymbol{P} = \sum_{l_1,l_2} \sum_{m_1, m_2} \mathcal{P}^{(l_1,l_2)}_{m_1m_2} \odot | l_1, m_1\rangle \langle l_2, m_2|

这里使用的 ⊙\odot 并不严谨，完全是为了让与分析无关的径向分量不出现在眼前而已，否则需要每时每刻都带上 n1,n2\bm{n_1,n_2}，张量的下标也会变多。不过这样处理后美观易读，是值得的。

旋转后的密度矩阵

  从现在开始，一个张量，如 Pm1m2(l1,l2),Dm′m(l)\displaystyle \bm{\mathcal{P^{(l_1,l_2)}_{m_1m_2}, D^{(l)}_{m'm}}}，以逗号分隔、括号包围的标记表示归属；没有逗号和括号的标记表示这一归属下的分量。

  在 密度矩阵的等变性 一节所定义的旋转算符 T^\hat T 以及它在一组基下的展开 TijT_{ij} 实际上有更细致的表达。若角动量经历一次旋转操作 R^(α,β,γ)\hat R(\alpha, \beta, \gamma)，旋转的效果将由 Wigner D-矩阵描述，它的定义为：

Dm′m(l)(α,β,γ)≡⟨l,m′∣R^(α,β,γ)∣l,m⟩ D_{m^\prime m}^{(l)}(\alpha, \beta, \gamma) \equiv\left\langle l, m^{\prime}\right| \hat{R}(\alpha, \beta, \gamma)|l ,m\rangle

所以旋转前后角动量波矢有如下的线性组合关系：

∣l,m⟩=∑m′∣l,m′⟩⟨l,m′∣l,m⟩=∑m′Dm′m(l)∣l,m′⟩ |l,m\rangle = \sum_{m'} |l,m'\rangle\langle l,m' | l,m \rangle = \sum_{m'} D_{m'm}^{(l)} |l,m'\rangle

对于同一分子轨道 ∣χi⟩|\chi_i\rangle，用旋转后的基组展开，则有

∣χi⟩=∑n∑l,mCnlm(i)∣n⟩⊗∑m′Dm′m(l)∣l,m′⟩=∑n∑l,mCnlm(i)∑m′Dm′m(l)∣n,l,m′⟩ |\chi_i\rangle = \sum_n\sum_{l,m} C^{(i)}_{nlm} |n\rangle \otimes \sum_{m'} D_{m'm}^{(l)} |l,m'\rangle = \sum_n\sum_{l,m} C^{(i)}_{nlm} \sum_{m'}D_{m'm}^{(l)} |n,l,m'\rangle

所以旋转后的密度矩阵为

P′=∑i∑n1,n2∑l1,l2∑m1,m2∑m1′,m2′Cn1l1m1(i)Cn2l2m2(i)∗Dm1′m1(l1)Dm2′m2(l2)∗∣n1,l1,m1′⟩⟨n2,l2,m2′∣=∑l1,l2∑m1′,m2′[∑m1,m2Dm1′m1(l1)Dm2′m2(l2)∗Pm1m2(l1,l2)]⊙∣l1,m1′⟩⟨l2,m2′∣\begin{aligned} \boldsymbol{P'} &= \sum_i \sum_{n_1,n_2}\sum_{l_1,l_2}\sum_{m_1,m_2}\sum_{m_1',m_2'} C^{(i)}_{n_1 l_1 m_1} C^{(i)*}_{n_2 l_2 m_2} D_{m_1'm_1}^{(l_1)}D_{m_2'm_2}^{(l_2)*} |n_1, l_1, m'_1\rangle \langle n_2, l_2, m'_2| \\ &= \sum_{l_1,l_2} \sum_{m'_1, m'_2} \left[ \sum_{m_1,m_2} D_{m_1'm_1}^{(l_1)}D_{m_2'm_2}^{(l_2)*} \mathcal{P}^{(l_1,l_2)}_{m_1m_2}\right] \odot |l_1, m'_1\rangle \langle l_2, m'_2| \end{aligned}

容易发现，这是等变性的分块形式，即对应每一个 (l1,l2)(l_1,l_2) 块 P(l1,l2)\mathcal{P}^{(l_1,l_2)}，旋转时有如下关系：

P(l1,l2)⇒D(l1)P(l1,l2)D(l2)† \mathcal{P}^{(l_1,l_2)} \quad \Rightarrow \quad D^{(l_1)} \mathcal{P}^{(l_1,l_2)} D^{(l_2)\dagger}

其中 D(l1),D(l2)D^{(l_1)}, D^{(l_2)} 的形状分别是 (2l1+1)×(2l1+1)(2l_1 + 1)\times (2l_1 +1) 和 (2l2+1)×(2l2+1)(2l_2 + 1)\times (2l_2 +1)，是正方形的；而 P(l1,l2)\mathcal{P}^{(l_1,l_2)} 不在对角时则是长方形的。

不可约表示分解

  在所有的 (2l1+1)×(2l2+1)(2l_1 + 1)\times (2l_2 +1) 矩阵所构成的线性空间 V(l1,l2)V^{(l_1,l_2)} 中定义线性作用 D(α,β,γ)\mathscr{D}(\alpha, \beta, \gamma)，对于其中的元素 P(l1,l2)\mathcal{P}^{(l_1,l_2)}，它的效果为

D(α,β,γ):    P(l1,l2)↦D(l1)(α,β,γ)  P(l1,l2)  D(l2)†(α,β,γ) \mathscr{D}(\alpha, \beta, \gamma):\;\; \mathcal{P}^{(l_1,l_2)} \mapsto D^{(l_1)}(\alpha, \beta, \gamma) \; \mathcal{P}^{(l_1,l_2)} \; D^{(l_2)\dagger}(\alpha, \beta, \gamma)

如此，前式可改写为

P′=∑l1,l2∑m1′,m2′D[P(l1,l2)]⊙∣l1,m1′⟩⟨l2,m2′∣ \boldsymbol{P'} = \sum_{l_1,l_2} \sum_{m'_1, m'_2} \mathscr{D} \Big[\mathcal{P}^{(l_1,l_2)}\Big] \odot |l_1, m'_1\rangle \langle l_2, m'_2|

可以证明线性作用 D(α,β,γ)\mathscr{D}(\alpha, \beta, \gamma) 是 SO(3)SO(3) 群在 V(l1,l2)V^{(l_1,l_2)} 上的实现，是群的表示。定义双线性函数 ⟨A,B⟩\langle A, B\rangle

⟨A,B⟩=∑i,jAijBij∗=Tr(AB†) \langle A, B\rangle = \sum_{i,j}A_{ij}B_{ij}^* = \text{Tr}(A B^\dagger)

其正定而对称，故为 V(l1,l2)V^{(l_1,l_2)} 上的内积。据此， V(l1,l2)V^{(l_1,l_2)} 上存在一组标准正交基，任何元素可因之展开。

  群表示论证明了表示空间 V(l1,l2)V^{(l_1,l_2)} 可以分解为 SO(3)SO(3) 群不可约表示空间的直和：

V(l1,l2)=⨁L=∣l1−l2∣∣l1+l2∣U(L) V^{(l_1,l_2)} = \bigoplus_{L=|l_1 - l_2|}^{|l_1 + l_2|} U^{(L)}

其中直和 ⊕\oplus 的定义为，对于任意 V(l1,l2)V^{(l_1,l_2)} 中的元素 P\mathcal{P}，存在如下的唯一分解：

∀P∈V(l1,l2),P=∑L=∣l1−l2∣∣l1+l2∣U(L),U(L)∈U(L) \forall \mathcal{P} \in V^{(l_1,l_2)}, \quad \mathcal{P} = \sum_{L=|l_1 - l_2|}^{|l_1 + l_2|} \mathcal{U}^{(L)}, \quad \mathcal{U}^{(L)} \in U^{(L)}

每一个归属于 U(L)U^{(L)} 不可约表示子空间中的元素 U(L)\mathcal{U}^{(L)} 均可在 U(L)U^{(L)} 的标准正交基组 {T(L,M,l1,l2)}\big\{\mathcal{T}^{(L,M, l_1, l_2)}\big\} 下展开：

U(L)=∑M=12L+1⟨T(L,M,l1,l2),P(l1,l2)⟩T(L,M,l1,l2) \mathcal{U}^{(L)} = \sum_{M=1}^{2L+1}\Big\langle\mathcal{T}^{(L,M, l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle \mathcal{T}^{(L, M, l_1, l_2)}

其中，{T(L,M,l1,l2)}\{\bm{\mathcal{T^{(L,M, l_1, l_2)} \}}} 称球谐张量，内积部分 ⟨T(L,M,l1,l2),P(l1,l2)⟩\bm{\displaystyle \Big\langle \mathcal{T}^{(L,M, l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle} 即是 Clebsch–Gordan 系数，恰同构于物理定义：

Cl1m1l2m2LM≡⟨L,M∣l1,m1,l2,m2⟩ C_{l_1m_1l_2m_2}^{LM} \equiv \langle L,M | l_1,m_1,l_2,m_2 \rangle

Clebsch–Gordan 系数对于确定的 LL 而言共有 2L+12L+1 个。由于作用 D\mathscr{D} 具有线性性，并且每一个不可约子空间都是 D\mathscr{D} 的不变子空间，所以在每一个子空间内都存在子矩阵 D(L)D^{(L)}，使得 D\mathscr{D} 在选定子空间一组基后的作用效果可以用矩阵乘以展开系数的形式表示：

D(P)=∑L=∣l1−l2∣∣l1+l2∣D(∑M=12L+1⟨T(L,M,l1,l2),P(l1,l2)⟩T(L,M,l1,l2))=∑L=∣l1−l2∣∣l1+l2∣∑M=12L+1(∑M′=12L+1DMM′(L)⟨T(L,M′,l1,l2),P(l1,l2)⟩) Tm1′m2′(L,M,l1,l2)\begin{aligned} \mathscr{D}(\mathcal{P}) &= \sum_{L=|l_1 - l_2|}^{|l_1 + l_2|} \mathscr{D} \left( \sum_{M=1}^{2L+1}\Big\langle\mathcal{T}^{(L, M, l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle \mathcal{T}^{(L, M, l_1, l_2)} \right) \\ &= \sum_{L=|l_1 - l_2|}^{|l_1 + l_2|} \sum_{M=1}^{2L+1} \bigg(\sum_{M'=1}^{2L+1} D^{(L)}_{MM'}\Big\langle \mathcal{T}^{(L,M', l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle\bigg) \, \mathcal{T}^{(L,M, l_1, l_2)}_{m_1'm_2'} \end{aligned}

由于 SO(3)\bm{SO(3)} 群独特的性质，线性作用 D\bm{\mathscr{D}} 在 U(L)\bm{U^{(L)}} 的实现矩阵 D(L)\bm{D^{(L)}} 正是对应的 Wigner D-矩阵。

  将以上结果带入密度矩阵，则密度矩阵按照角动量耦合而自然分块的不可约表示分解如下：

P′=∑l1,l2∑m1′,m2′[∑L,M(∑M′DMM′(L)⟨T(L,M′,l1,l2),P(l1,l2)⟩) Tm1′m2′(L,M,l1,l2)]⊙∣l1,m1′⟩⟨l2,m2′∣ \boldsymbol{P'} = \sum_{l_1,l_2} \sum_{m'_1, m'_2} \Bigg[\sum_{L,M} \bigg(\sum_{M'}D^{(L)}_{MM'}\Big\langle \mathcal{T}^{(L,M', l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle\bigg) \, \mathcal{T}^{(L,M, l_1, l_2)}_{m_1'm_2'}\Bigg] \odot |l_1, m'_1\rangle \langle l_2, m'_2|

上式有四层含义：

  • 密度矩阵按照角动量 l1,l2l_1,l_2 分块；
  • 每一个 (l1,l2)(l_1,l_2) 块 P(l1,l2)\mathcal{P}^{(l_1,l_2)} 可做 SO(3)SO(3) 群不可约表示分解；
  • 每一个不可约子空间中存在球谐张量基组 {T(L,M,l1,l2)}\big\{\mathcal{T}^{(L,M, l_1, l_2)}\big\}；
  • 密度矩阵的旋转对应于展开系数 ⟨T(L,M′,l1,l2),P(l1,l2)⟩\Big\langle \mathcal{T}^{(L,M', l_1, l_2)}, \mathcal{P}^{(l_1,l_2)}\Big\rangle 的线性变换。

故曰：密度矩阵通过 Clebsch–Gordan 展开系数实现参数化。

球谐张量的确定

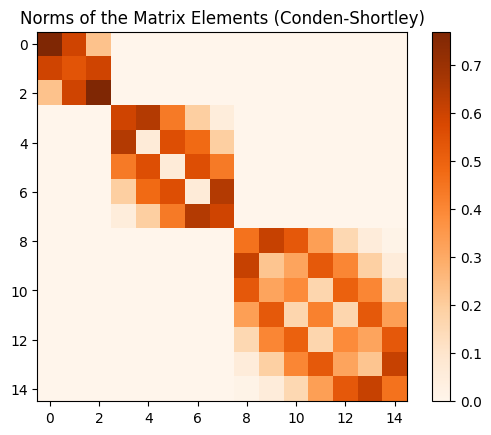
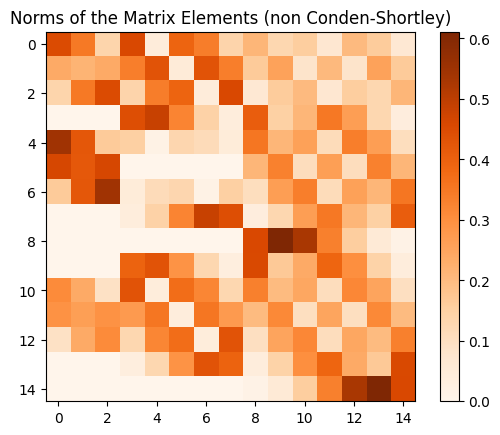
  计算球谐张量 T(L,M,l1,l2)\bm{\mathcal{T^{(L,M, l_1, l_2)}}} 的分量等价于寻找球谐张量在自然基组下的展开系数，其中 3.2 节详细阐述了 Conden-Shortley 约定。。为此，我们先来研究线性作用 D\mathscr{D} 在球谐张量基组 {T(L,M,l1,l2)}\big\{\mathcal{T}^{(L,M, l_1, l_2)}\big\} 下对应矩阵之形貌。

  表示空间 V(l1,l2)V^{(l_1,l_2)} 存在自然标准正交基 {Vj}\{\mathcal{V}_j\}

V1=[10⋯000⋯0⋮⋮⋱⋮],V2=[01⋯000⋯0⋮⋮⋱⋮],⋯ ,V(2l1+1)×(2l2+1)=[00⋯000⋯0⋮⋮⋱1] \mathcal{V}_1 = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ \end{bmatrix}, \quad \mathcal{V}_2 = \begin{bmatrix} 0 & 1 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ \end{bmatrix}, \quad \cdots, \quad \mathcal{V}_{(2l_1+1)\times(2l_2+1)} = \begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & 1 \\ \end{bmatrix}

设新基 {Ui}\{\mathcal{U}_i\} 与这组自然基之间的过渡矩阵为 TT，有 Ui=∑TijVj\mathcal{U}_i = \displaystyle\sum T_{ij} \mathcal{V}_j。由于 D\mathscr{D} 是群的表示，对它进行不可约分解等价于线性作用 D\mathscr{D} 在这组新基 {Ui}\{\mathcal{U}_i\} 下对应的矩阵采取分块对角化的形式。 显然，自然基 {Vj}\{\mathcal{V}_j\} 对应于 ∣l1,m1,l2,m2⟩| l_1, m_1, l_2, m_2 \rangle ，而新基对应球谐张量 ∣L,M,l1,l2⟩|L,M, l_1, l_2 \rangle ，按照角动量将下标重新排列，则可以将 ii 更换为 L,ML,M、jj 更换为 m1,m2m_1,m_2、对 jj 求和更换为对 m1,m2m_1,m_2 求和：

U(L,M)=∑m1,m2Tm1m2(L,M)Vm1m2 \mathcal{U}^{(L,M)} = \sum_{m_1,m_2} T_{m_1m_2}^{(L,M)} \mathcal{V}_{m_1m_2}

采取前文记法，则有

∣L,M,l1,l2⟩=∑m1,m2Tm1m2(L,M,l1,l2)∣l1,m1,l2,m2⟩ |L,M, l_1, l_2 \rangle = \sum_{m_1,m_2} \mathcal{T}_{m_1m_2}^{(L,M,l_1,l_2)} |l_1, m_1, l_2, m_2\rangle

同时左乘 ⟨l1,n1,l2,n2∣\langle l_1, n_1, l_2, n_2 |，得到

⟨l1,n1,l2,n2∣L,M,l1,l2⟩=∑m1,m2Tm1m2(L,M,l1,l2)⟨l1,n1,l2,n2∣l1,m1,l2,m2⟩=Tn1n2(L,M,l1,l2) \langle l_1, n_1, l_2, n_2 | L, M, l_1, l_2 \rangle = \sum_{m_1,m_2} \mathcal{T}_{m_1m_2}^{(L,M,l_1,l_2)} \langle l_1, n_1, l_2, n_2 | l_1, m_1, l_2, m_2\rangle = \mathcal{T}_{n_1n_2}^{(L,M,l_1,l_2)}

等号左边 ⟨l1,n1,l2,n2∣L,M,l1,l2⟩\langle l_1, n_1, l_2, n_2 | L, M, l_1, l_2 \rangle 即是标准的 Clebsch–Gordan 系数，保存在多种数学软件中。考虑在确定球谐函数时常用的 Conden-Shortley 约定，最终的球谐张量如下式：

Tm1m2(L,M,l1,l2)=(−1)(l2−m2)C(L,M,l1,m1,l2,−m2) \mathcal{T}_{m_1m_2}^{(L,M,l_1,l_2)} = (-1)^{(l_2 - m_2)}C(L,M,l_1,m_1,l_2,-m_2)

如此，在这组球谐张量基下，线性作用 D\mathscr{D} 的矩阵是对角块的直和 ⨁L=∣l1−l2∣∣l1+l2∣D(L)\displaystyle\bigoplus_{L=|l_1-l_2|}^{|l_1+l_2|} D^{(L)}。如图。

equivariance1

equivariance2